equation through which we can define the conduction in any shape of body and we
can calculate the temperature at any point in a medium in any situation like
steady flow, transient flow, one dimension flow, three dimension flow etc. It
is governing equation of conduction.
There
are various shapes of body such as rectangular shape, cylindrical shape,
spherical shape and combine shape. All the
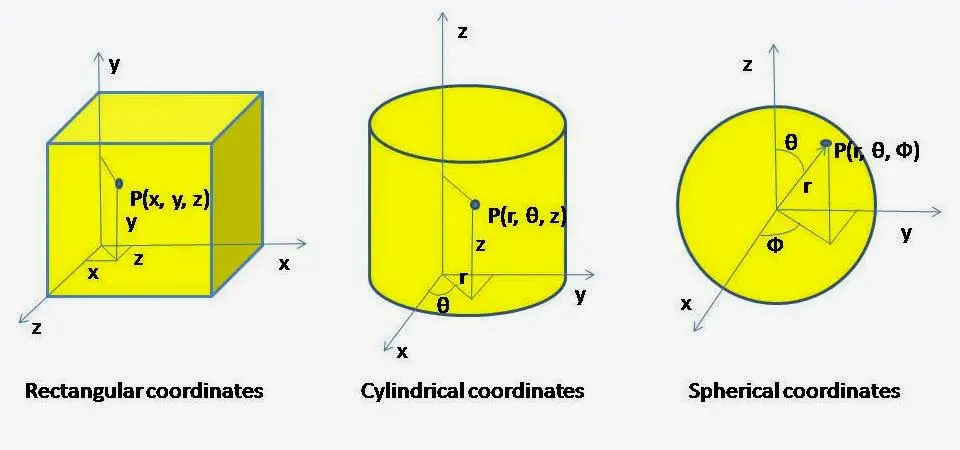
shape or any point in a body can be represented by three coordinates system. They
may be rectangular coordinate for rectangular shape, spherical coordinate for
spherical shape and cylindrical coordinate for cylindrical shape.
Heat conduction equation for rectangular coordinate
a body which is represent by rectangular coordinate then we have to use
rectangular heat conduction equation which is given by:
conditions. Some of them are given below:
- For constant thermal conductivity:
- For steady state ( ∂T / ∂t = 0 ):
- For no heat generation ( e = 0 )
Heat conduction equation for cylindrical coordinates
we have to use cylindrical heat conduction equation which is given by:
Heat conduction equation for
spherical coordinates
When
we want to define conduction in spherical body then we have to use
spherical heat conduction equation which
is given by
differential equations are solved by the use of two boundary conditions. The mathematical
expression of thermal condition at the boundary is known as boundary condition.
Some of boundary conditions for one dimension heat conduction are given below.
the temperature of both end are known.
the heat enter and heat rejected by the surface or heat flux are known.
the boundary is insulated at one end, then heat transfer at that end becomes equal to
zero.
the surface is exposed into environment then heat transfer by conduction equal
to heat transfer by convection.
Practical use of heat conduction equation
Problem:-
Consider the base plate of a 1200W household iron that has a thickness of 5 mm, base area of 300cm2 and thermal conductivity of metal 15W/m-k. The inner surface of the base plate is subjected to uniform heat flux generate by resistance heater inside, and the outer surface loss the heat to surrounding at temperature 200C by convection. Taking the convection coefficient to be 80W/m2k and disregarding heat loss by radiation. Obtain an expression for the variation of temperature in the base plate and the temperature at the outer surface and inner surface.
Solution:
Given:
Total heat transfer rate, Q = 1200W
Thermal conductivity of base plate ,k = 15W/m-k
Surrounding temperature, Ts = 200C
Convection coefficient, h = 80W/m2k
Surface area of base plate, A = 300cm2 = 0.03m2
Outer surface temperature, To = ?
Because every point of base plate of iron can be easily described by a rectangular coordinate.And We know that heat transfer equation in rectangular coordinate is given by:-
some conditions as below-
is steady so, ∂T / ∂t = 0.
base plate of iron is very large then its thickness so heat transfer is one dimension. This implies
and ∂T /∂z = 0
in base plate is zero.
coefficient is constant.
conduction equation reduces to
equation first take it’s integral. The general solution of it is:
C2 are integration constant. To find this constant we have to use boundary
conditions. Here are two boundary conditions.
Heat transfer
rate at inner surface.
surface is exposed in environment so heat transfer by conduction is equal to
heat transfer by convection.
temperature variation is given by
surface temperature
surface temperature

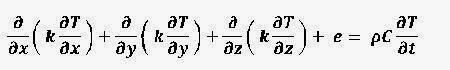

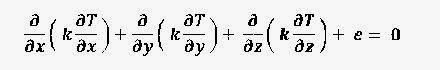
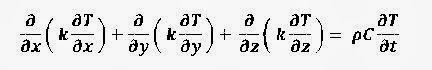


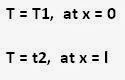
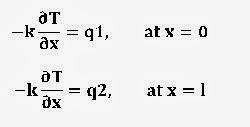
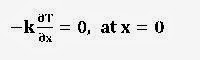
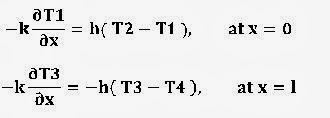
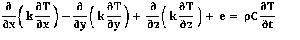
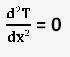

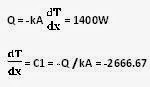
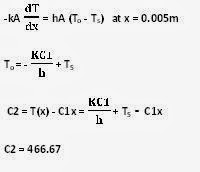
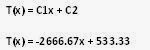
.bmp)







