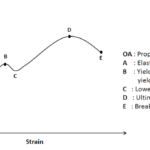
The concept of elasticity and Young’s modulus can be traced back to the 18th century. Thomas Young, a British polymath, introduced the concept in 1807. He conducted experiments on the deformation of solid materials and proposed a relationship between stress and strain. Young’s work laid the foundation for understanding the elastic behavior of materials.
Young’s modulus, also known as the elastic modulus or the modulus of elasticity, is a mechanical property that describes the stiffness or elasticity of a material. It measures the ratio of stress to strain within the elastic limit of a material. The concept of Young’s modulus has a rich history and plays a crucial role in material science, engineering, and various applications.
Furthermore, in this article basic definition of Young’s modulus, its role, advantages and disadvantages, and a detailed explanation with the help of examples will be discussed.
What is Young’s Modulus?
Young’s modulus, also known as the elastic modulus / modulus of elasticity, is a mechanical property that describes the stiffness or rigidity of a material.
Young’s modulus specifically relates to the linear elasticity of a material, which means it applies when the object deforms elastically under applied stress and returns to its original shape once the stress is removed.
Mathematically, Young’s modulus (E) is calculated as:
E = (stress)/(strain)
where stress is the applied force per unit area (force divided by the cross-sectional area of the material) on the other hand strain is the ratio of the change in length to the original length of the material.
Young’s modulus is typically expressed in units of pressure, such as pascals (Pa) or megapascals (MPa). It is a fundamental property of a material and provides insight into how the material will respond to applied forces, particularly in terms of how much it will deform or elongate under stress.
Materials with higher Young’s modulus values are stiffer and less deformable, while materials with lower Young’s modulus values are more flexible and easily deformable.
Role:
Young’s modulus is a fundamental parameter in material science and engineering. It plays a significant role in the following aspects:
Young’s modulus helps engineers and designers in selecting appropriate materials for specific applications. Different materials have different stiffness properties, and knowing Young’s modulus enables engineers to choose materials that can withstand the required loads and deformations.
Young’s modulus is essential in designing structures such as bridges, buildings, and mechanical components. By considering the elastic modulus, engineers can ensure that the materials used have the necessary stiffness to bear the anticipated loads and deformations without failure or excessive deflection.
Young’s modulus is a crucial parameter for characterizing materials. It provides information about a material’s response to applied forces, its ability to store and release elastic energy, and its overall mechanical behavior.
Advantages of Young’s Modulus
Young’s modulus offers several advantages in engineering and materials science:
Young’s modulus allows engineers to predict the amount of deformation a material will experience when subjected to external forces. This information is crucial for designing structures that maintain their shape and integrity under various loading conditions.
Young’s modulus enables direct comparison of the stiffness of different materials. It helps identify which material is more suitable for a particular application based on its ability to resist deformation and support loads.
By understanding the relationship between Young’s modulus and other mechanical properties, engineers can optimize material compositions and structures to achieve desired stiffness, strength, and durability characteristics.
Disadvantages of Young’s Modulus
While Young’s modulus is a valuable parameter, it also has limitations:
Young’s modulus assumes that the material behaves elastically within its linear range. It does not account for non-linear behavior, plastic deformation, or failure mechanisms that can occur at high stresses or strains.
Young’s modulus represents the average stiffness of a material. In real-world scenarios, materials can exhibit different stiffness properties in different directions due to anisotropy. Young’s modulus alone may not fully capture the complex mechanical behavior of anisotropic materials.
Young’s modulus is typically determined under specific environmental conditions. However, temperature and moisture can significantly influence a material’s stiffness, leading to variations in its elastic modulus. These effects need to be considered for accurate material characterization and design.
How to calculate Young’s modulus?
Here are a few examples
Example 1:
Calculate Young’s modulus if the applied stress is 8 N/m2 to produce a strain of 0.4.
Ans:
Data given:
σ = 8 N/m2
ε = 0.4
The formula for Young’s modulus is mentioned below;
E = σ / ϵ
Using the values
= 8 / 0.4
=20 N/m2
Hence, Young’s modulus is 20 N/m2
You can also try a young modulus calculator to deal with the above kind of problems and get the result in a few seconds by placing the values of stress and strain into the required boxes.
Example 2:
Calculate Young’s modulus if the applied stress is 10 N/m2 to produce a strain of 0.1.
Ans:
Data given:
σ = 10 N/m2
ε = 0.1
The formula for Young’s modulus is mentioned below;
E = σ / ϵ
Using the values
= 10 / 0.1
= 100 N/m2
Hence Young’s modulus is 100 N/m2
Example 2:
Calculate Young’s modulus if the applied stress is 30 N/m2 to produce a strain of 0.2.
Ans:
Data given:
σ = 30 N/m2
ε = 0.2
The formula for Young’s modulus is mentioned below;
E = σ / ϵ
Using the values
= 30 / 0.2
= 150 N/m2
Hence Young’s modulus is 150 N/m2
Conclusion:
In this article, the history of Young’s modulus basic definition role of Young’s modulus advantages and disadvantages are discussed. Moreover, for a better understanding of the topic with the help of examples, a few problems are solved to calculate Young’s modulus.