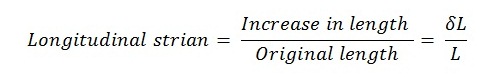In this article, you will learn about what is poisson’s ratio, longitudinal Strain and lateral strain. We will also find the formula of Poisson’s ratio, lateral strain and longitudinal strain.
What is Poisson’s Ratio
Poisson’s Ratio: It is defined as the ratio of lateral strain to the longitudinal strain within elastic limit. It means that when a material is loaded within elastic limit than the ratio of lateral strain to the longitudinal strain gives us a constant called poisson’s ratio.
It is denoted by the symbol μ.
The value of poisson’s ratio varies from 0.25 to 0.33. For rubber its value varies from 0.45 to 0.50.
Mathematically
Here we encountered with two terms lateral strain and longitudinal strain. Let’s understand about them.
Longitudinal Strain
When an axial tensile or compressive load is applied on a body, then there is an axial deformation appears in the length of the body. The ratio of axial deformation to the original length of the body is called as longitudinal strain.
It is also defined as the deformation per unit length in the direction of the applied load.
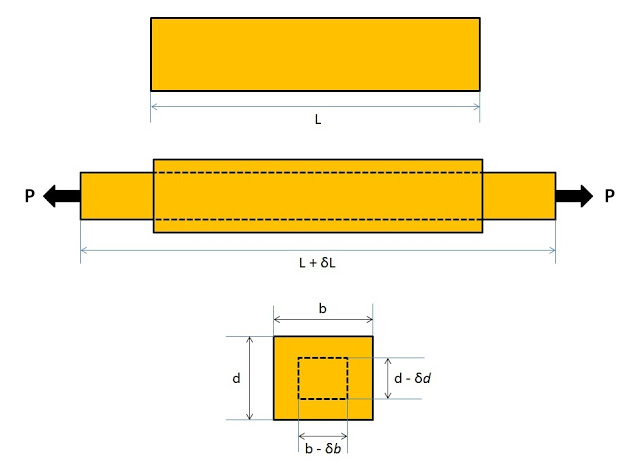
Considered a body having length L and axial tensile load P is applied on it. There is an increase in the length of the body in the direction of the applied load as shown in the figure ‘a’ given below.
Let
L = Length of the body
P = Tensile load acting on the body
δL = increase in the length of the body in the direction of P
When an axial tensile load is applied on a body, there is an increase in the length of the body. But at the same time, other dimensions which are at right angles to the line of action of the applied load decreases. The strain which produced at right angles to the direction of the applied load is known as lateral strain.
Considered a rectangular bar having length L, breadth b and depth d are subjected to an axial tensile load P as shown in the figure given below.
a
Let
δL = increase in length
δb = decrease in breadth, and
δd = decrease in depth.
The lateral strain is of opposite kind i.e. if the longitudinal strain is tensile (compressive), the lateral strain will be compressive (tensile). So from the formula of Poisson’s ratio, algebraically lateral strain can also be expressed as
Lateral strain= -μ x Longitudinal strain
Here the minus sign is used to indicate the opposite nature of both the lateral and longitudinal strain.
Points to Remember
If the longitudinal strain is tensile, then the lateral strain will be compressive.
If the lateral strain is tensile, then the longitudinal strain will be compressive.
A longitudinal strain in the direction of applied load is every time accompanied by an equal and opposite lateral strain at right angle to the applied load.
For better explanation watch the video given below:
In this article, we have learned about what is Poisson’s ratio and its formula? We have also learned about the longitudinal strain and lateral strain. If you find a query then comment us. And if you like the article then like and share it.
